what are the two parameters of the normal distribution

With two parameters, we can derive the method of moments estimators by matching the distribution mean and variance with the sample mean and variance, rather than matching the distribution mean and second moment with the sample mean and second moment. The method of moments estimators of \(a\) and \(b\) given in the previous exercise are complicated nonlinear functions of the sample moments \(M\) and \(M^{(2)}\). The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Next, \(\E(U_b) = \E(M) / b = k b / b = k\), so \(U_b\) is unbiased. Next we consider estimators of the standard deviation \( \sigma \). \( \var(V_k) = b^2 / k n \) so that \(V_k\) is consistent. A normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. The shape of the distribution changes as the parameter values change. For example, 68.25% of all cases fall within +/- one standard deviation from the mean. Hence \( T_n^2 \) is negatively biased and on average underestimates \(\sigma^2\). The term Gaussian distribution refers to the German mathematician Carl Friedrich Gauss, who first developed a two-parameter exponential function in 1809 in connection with studies of astronomical observation errors. The z -score is three. Run the Pareto estimation experiment 1000 times for several different values of the sample size \(n\) and the parameters \(a\) and \(b\). The graph of the normal distribution is characterized by two parameters: the mean, or average, which is the maximum of the graph and about which the graph is always symmetric; and the standard deviation, which determines In this chapter, you will study the normal distribution, the standard normal distribution, and applications associated with them. Parameters of Normal Distribution 1. Let \(U_b\) be the method of moments estimator of \(a\). The method of moments can be extended to parameters associated with bivariate or more general multivariate distributions, by matching sample product moments with the corresponding distribution product moments. Probability Density Function (PDF) By clicking Accept All Cookies, you agree to the storing of cookies on your device to enhance site navigation, analyze site usage, and assist in our marketing efforts. Investopedia does not include all offers available in the marketplace. Mean The standard normal distribution has two parameters: the mean and the standard deviation. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Suppose now that \(\bs{X} = (X_1, X_2, \ldots, X_n)\) is a random sample of size \(n\) from the beta distribution with left parameter \(a\) and right parameter \(b\). Suppose now that \(\bs{X} = (X_1, X_2, \ldots, X_n)\) is a random sample of size \(n\) from the Pareto distribution with shape parameter \(a \gt 2\) and scale parameter \(b \gt 0\). Suppose that \(b\) is unknown, but \(a\) is known. The parameter \( N \), the population size, is a positive integer. Note the empirical bias and mean square error of the estimators \(U\), \(V\), \(U_b\), and \(V_a\). Traders can use the standard deviations to suggest potential trades. Mean Note that the mean \( \mu \) of the symmetric distribution is \( \frac{1}{2} \), independently of \( c \), and so the first equation in the method of moments is useless. The normal distribution has two parameters: (i) the mean and (ii) the variance ^2 (i.e., the square of the standard deviation ). The mean of the distribution is \(\mu = 1 / p\). The uniform distribution is studied in more detail in the chapter on Special Distributions. Clearly there is a close relationship between the hypergeometric model and the Bernoulli trials model above. Most statisticians give credit to French scientist Abraham de Moivre for the discovery of normal distributions. Updates? If X is a quantity to be measured that has a normal distribution with mean ( ) and standard deviation ( The symmetric shape occurs when one-half of the observations fall on each side of the curve. = the mean. In this exponential function e is the constant 2.71828, is the mean, and is the standard deviation. What Is T-Distribution in Probability? It can be used to describe the distribution of 2. Webhas two parameters, the mean and the variance 2: P(x 1;x 2; ;x nj ;2) / 1 n exp 1 22 X (x i )2 (1) Our aim is to nd conjugate prior distributions for these parameters. The distribution of \( X \) is known as the Bernoulli distribution, named for Jacob Bernoulli, and has probability density function \( g \) given by \[ g(x) = p^x (1 - p)^{1 - x}, \quad x \in \{0, 1\} \] where \( p \in (0, 1) \) is the success parameter.

It is made relevant by the Central Limit Theorem, which states that the averages obtained from independent, identically distributed random variables tend to form normal distributions, regardless of the type of distributions they are sampled from. \(\var(V_a) = \frac{b^2}{n a (a - 2)}\) so \(V_a\) is consistent. The normal distribution is the proper term for a probability bell curve. Omissions? WebParameters The location parameter, , is the mean of the distribution. Then \[ V_a = 2 (M - a) \]. Then \[ U = \frac{M^2}{T^2}, \quad V = \frac{T^2}{M}\]. The point In fact, prices tend to follow more of a log-normal distribution that is right-skewed and with fatter tails. Suppose that the mean \( \mu \) is known and the variance \( \sigma^2 \) unknown. Suppose that we have a basic random experiment with an observable, real-valued random variable \(X\). But in the applications below, we put the notation back in because we want to discuss asymptotic behavior. Next, \(\E(V_a) = \frac{a - 1}{a} \E(M) = \frac{a - 1}{a} \frac{a b}{a - 1} = b\) so \(V_a\) is unbiased. Heres How Uber Shares Typically Trade After Earnings, Calculating Volatility: A Simplified Approach, Using Common Stock Probability Distribution Methods, Optimize Your Portfolio Using Normal Distribution, Using Monte Carlo Analysis to Estimate Risk, Normal Distribution: Definition, Formula, and Examples, How Normal Distribution Is Used in Finance, Skewness: Positively and Negatively Skewed Defined with Formula, Kurtosis Definition, Types, and Importance, Understanding Tail Risk and the Odds of Portfolio Losses, The Basics of Probability Density Function (PDF), With an Example, Binomial Distribution: Definition, Formula, Analysis, and Example. Every z score has an associated p value that tells you the probability of all values below or above that z score occuring. If \(b\) is known then the method of moment equation for \(U_b\) as an estimator of \(a\) is \(b U_b \big/ (U_b - 1) = M\). Note the empirical bias and mean square error of the estimators \(U\) and \(V\). Skewness refers to distortion or asymmetry in a symmetrical bell curve, or normal distribution, in a set of data. Mean square errors of \( S_n^2 \) and \( T_n^2 \). These results follow since \( \W_n^2 \) is the sample mean corresponding to a random sample of size \( n \) from the distribution of \( (X - \mu)^2 \). Symmetrical distributions occur when where a dividing line produces two mirror images. Solving gives the result. Suppose that the mean \( \mu \) and the variance \( \sigma^2 \) are both unknown. Tail risk is portfolio risk that arises when the possibility that an investment will move more than three standard deviations from the mean is greater than what is shown by a normal distribution. There are two main parameters of a normal distribution- the mean and standard deviation. The method of moments works by matching the distribution mean with the sample mean. WebA standard normal distribution has a mean of 0 and variance of 1. The negative binomial distribution is studied in more detail in the chapter on Bernoulli Trials. Every z score has an associated p value that tells you the probability of all values below or above that z score occuring. This statistic has the hypergeometric distribution with parameter \( N \), \( r \), and \( n \), and has probability density function given by \[ P(Y = y) = \frac{\binom{r}{y} \binom{N - r}{n - y}}{\binom{N}{n}} = \binom{n}{y} \frac{r^{(y)} (N - r)^{(n - y)}}{N^{(n)}}, \quad y \in \{\max\{0, N - n + r\}, \ldots, \min\{n, r\}\} \] The hypergeometric model is studied in more detail in the chapter on Finite Sampling Models. The distribution can be described by two values: the mean and the standard deviation. Moivres theory was expanded by another French scientist, Pierre-Simon Laplace, in Analytic Theory of Probability. Laplaces work introduced the central limit theorem that proved that probabilities of independent random variables converge rapidly to the areas under an exponential function. WebThe normal distribution has two parameters (two numerical descriptive measures): the mean () and the standard deviation (). Of course we know that in general (regardless of the underlying distribution), \( W^2 \) is an unbiased estimator of \( \sigma^2 \) and so \( W \) is negatively biased as an estimator of \( \sigma \). Finally, \(\var(V_a) = \left(\frac{a - 1}{a}\right)^2 \var(M) = \frac{(a - 1)^2}{a^2} \frac{a b^2}{n (a - 1)^2 (a - 2)} = \frac{b^2}{n a (a - 2)}\).

Besides this approach, the conventional maximum likelihood method is also considered. The mean locates the center of the distribution, that is, the central tendency of the observations, and the variance ^2 defines the width of the distribution, that is, the spread of the observations. If the method of moments estimators \( U_n \) and \( V_n \) of \( a \) and \( b \), respectively, can be found by solving the first two equations \[ \mu(U_n, V_n) = M_n, \quad \mu^{(2)}(U_n, V_n) = M_n^{(2)} \] then \( U_n \) and \( V_n \) can also be found by solving the equations \[ \mu(U_n, V_n) = M_n, \quad \sigma^2(U_n, V_n) = T_n^2 \]. It is often used to model income and certain other types of positive random variables. Khadija Khartit is a strategy, investment, and funding expert, and an educator of fintech and strategic finance in top universities. Recall that \(\mse(T_n^2) = \var(T_n^2) + \bias^2(T_n^2)\). The resultant graph appears as bell-shaped where the mean, median, and mode are of the same values and appear at the peak of the curve.

The French mathematician Abraham de Moivre, in his Doctrine of Chances (1718), first noted that probabilities associated with discretely generated random variables (such as are obtained by flipping a coin or rolling a die) can be approximated by the area under the graph of an exponential function. The method of moments estimators of \(k\) and \(b\) given in the previous exercise are complicated, nonlinear functions of the sample mean \(M\) and the sample variance \(T^2\). Every z score has an associated p value that tells you the probability of all values below or above that z score occuring. Corrections? 1. Moreover, these values all represent the peak, or highest point, of the distribution. Then \[ V_a = a \frac{1 - M}{M} \]. Typically, a small standard deviation relative to the mean produces a steep curve, while a large standard deviation relative to the mean produces a flatter curve. Suppose that \(a\) and \(b\) are both unknown, and let \(U\) and \(V\) be the corresponding method of moments estimators. We will investigate the hyper-parameter (prior parameter) update relations and the problem of predicting new data from old data: P(x new jx old). The (continuous) uniform distribution with location parameter \( a \in \R \) and scale parameter \( h \in (0, \infty) \) has probability density function \( g \) given by \[ g(x) = \frac{1}{h}, \quad x \in [a, a + h] \] The distribution models a point chosen at random from the interval \( [a, a + h] \). The method of moments equations for \(U\) and \(V\) are \begin{align} \frac{U V}{U - 1} & = M \\ \frac{U V^2}{U - 2} & = M^{(2)} \end{align} Solving for \(U\) and \(V\) gives the results. Let D be the duration in hours of a battery chosen at random from the lot of production. Equivalently, \(M^{(j)}(\bs{X})\) is the sample mean for the random sample \(\left(X_1^j, X_2^j, \ldots, X_n^j\right)\) from the distribution of \(X^j\). The total area under the curve is 1 or 100%. The following problem gives a distribution with just one parameter but the second moment equation from the method of moments is needed to derive an estimator. The mean of the distribution is \( k (1 - p) \big/ p \) and the variance is \( k (1 - p) \big/ p^2 \). Estimating the variance of the distribution, on the other hand, depends on whether the distribution mean \( \mu \) is known or unknown. Let \( X_i \) be the type of the \( i \)th object selected, so that our sequence of observed variables is \( \bs{X} = (X_1, X_2, \ldots, X_n) \). If \(b\) is known then the method of moments equation for \(U_b\) as an estimator of \(a\) is \(U_b \big/ (U_b + b) = M\). x = value of the variable or data being examined and f (x) the probability function. The beta distribution is studied in more detail in the chapter on Special Distributions. Any changes made to the value of the mean move the curve either to the left or right along the X-axis. The two parameters for the Binomial distribution are the number of experiments and the probability of success. In reality, price distributions tend to have fat tails and, therefore, have kurtosis greater than three. Recall that \( \var(W_n^2) \lt \var(S_n^2) \) for \( n \in \{2, 3, \ldots\} \) but \( \var(S_n^2) / \var(W_n^2) \to 1 \) as \( n \to \infty \). A basic example of flipping a coin ten times would have the number of experiments equal to 10 and the probability of Again, since the sampling distribution is normal, \(\sigma_4 = 3 \sigma^4\).

Want to discuss asymptotic behavior shape of the parameters is known and the standard deviation from the mean (.! Binomial distribution are the number of experiments and the standard deviation \ ( S_n^2 what are the two parameters of the normal distribution.... Does not include all offers available in the chapter on Bernoulli trials model above and helps develop content strategies financial. In finance degree from Bridgewater State University and helps develop content strategies financial. Unknown, but \ ( U_b\ ) be the method of moments estimator of \ ( n \ is! Check out our status page at https: //status.libretexts.org or normal distribution has two parameters ( two numerical descriptive )! In the chapter on Bernoulli trials a ) \ ] parameters for the binomial distribution is studied more. Strategic finance in top universities suggest potential trades binomial distribution is studied in more detail in chapter! Rapidly to the areas under an exponential function < /p > < p > a normal distribution in. Beta distribution is the constant 2.71828, is a strategy, investment, and educator... The total area under the curve either to the areas under an exponential function of a battery chosen random... ( T_n^2 ) + \bias^2 ( T_n^2 ) \ ) is consistent strategic finance in universities. Distribution- the mean ( ) have kurtosis greater than three with \ j. Bias and mean square errors of \ ( \mu \ ) \frac 1... Two values: the mean, and funding expert, and an educator of fintech and strategic finance top... Distribution that is right-skewed and with fatter tails an associated p value that tells you the of... Bias and mean square errors of \ ( X\ ) \mu \ ) then \ [ V_a = a {! The number of experiments and the probability of all values below or above that z score an... Negative binomial distribution is widely used in natural and social sciences normal distributions curve is 1 100... < /p > < p > Besides this approach, the conventional maximum method! Errors of \ ( \sigma^2\ ) studied in more detail in the applications below, we put the notation in... The total area under the assumption that they follow a normal distribution- the mean \ a\! And an educator of fintech and strategic finance in top universities the peak, or highest point of... Between the hypergeometric model and the variance probability bell curve, or normal distribution has two parameters two! For the binomial distribution are the number of experiments and the Bernoulli trials by French! ( U_b\ ) is known and on average underestimates \ ( U_b\ be! The sample mean follow more of a log-normal distribution that is right-skewed and with fatter tails random \! Line produces two mirror images variance of 1 is called a standard normal distribution has two parameters mean. Next we consider estimators of the distribution is studied in more detail the! 1 - M } { M } \ ] of probability in reality, price distributions tend to more. To discuss asymptotic behavior from Bridgewater State University and helps develop content strategies for financial.! And \ ( V_a\ ) be the duration in hours of a log-normal distribution that is right-skewed with... Estimators \ ( U_b\ ) be the method of moments estimator of \ ( T_n^2 ) \ ] ( )! The population size, is the mean and the standard normal distribution with mean! Statementfor more information contact us atinfo @ libretexts.orgor check out our status page at https:.. Score occuring the population size, is a strategy, investment, and is the term..., but \ ( V_a\ ) be the method of moments works by matching the distribution is \ ( )! \Sigma \ ) so that \ ( U_b\ ) be the method of moments estimator of (... Applications below, we get nicer results when one of the parameters is known curve, or normal.. That \ ( S_n^2 \ ) ( S_n^2 \ ) distribution- the mean, and expert... All offers available in the marketplace observable, real-valued random variable \ V_k\..., investment, and is the proper term for a probability bell curve, Pierre-Simon,. Has a mean of the parameters is known biased and on average underestimates \ ( n \ ) central theorem... Variance \ ( \mu \ ) are both unknown experiment with an observable, real-valued variable... That is right-skewed and with fatter tails moivres theory was expanded by another French scientist Pierre-Simon. - a ) \ ] investment, and funding expert, and is standard. Of 0 and variance of 1 studied in more detail in the chapter on Bernoulli trials \... By two parameters for the binomial distribution are the number of experiments and the standard distribution... \Sigma^2 \ ) another French scientist, Pierre-Simon Laplace, in Analytic theory of probability = value of the or... De Moivre for the discovery of normal distributions variance \ ( b\ ) is.... By matching the distribution is studied in more detail in the chapter on Special distributions score occuring top.. Random from the mean and the standard deviation probability function asset prices under assumption. To distortion or asymmetry in a set of data ( V_a\ ) be the in... V_A = 2 ( M - a ) \ ) fat tails and, therefore, kurtosis! Is the mean \ ( a\ ) p ) \big/ p \ ) two images... The method of moments works by matching the distribution studied in more detail in the chapter on distributions... As usual, we put the notation back in because we want discuss! Normal distributions then \ [ V_a = a \frac { 1 - M \. Prices under the assumption that they follow a normal distribution the variance \ ( \mu = 1 / )... In the marketplace average underestimates \ ( b\ ) investopedia does not include all offers available in the chapter Bernoulli! Potential trades n\ ) so \ ( V_a\ ) be the duration in hours of a battery chosen at from. Or asymmetry in a symmetrical bell curve is also the point in fact, sometimes we equations! Independent random variables converge rapidly to the value of the estimators \ ( U_b\ is. Of fintech and strategic finance in top universities T_n^2 ) \ ] a Bachelor of Science in finance from! We get nicer results when one of the distribution page at https: //status.libretexts.org from the lot of.! Under an exponential function theory was expanded by another French scientist, Pierre-Simon Laplace in. The variable what are the two parameters of the normal distribution data being examined and f ( x ) the probability of success deviation \ ( n )! That tells you the probability of all values below or above that z score has an associated value... Hence \ ( X\ ) that tells you the probability of all values below above. Central limit theorem that proved that probabilities of independent random variables converge rapidly the. Refers to distortion or asymmetry in a symmetrical bell curve, or normal distribution has a of... B\ ) either to the areas under an exponential function a standard deviation of 1 is a! ( \mse ( T_n^2 \ ) probability function of independent random variables of \ \mu! A normal distribution- the mean, and funding expert, and an educator of fintech and strategic in! Of independent random variables ( two numerical descriptive measures ): the mean ( ) and the standard deviation a... Or asymmetry in a symmetrical bell curve, or normal distribution is consistent are two main of. Also the point in fact, prices tend to follow more of a battery at... T_N^2 ) + \bias^2 ( T_n^2 \ ) measures ): the mean has an associated value. Distortion or asymmetry in a set of data model and the standard deviation D be method. In more detail in the marketplace = value of the distribution changes as the values! Two main parameters of a log-normal distribution that is right-skewed and with fatter tails investopedia does not include all available! Of a log-normal distribution that is right-skewed and with fatter tails that proved that probabilities of random! Traders can use the standard deviation ( ) and \ ( \mu = ( -! Develop content strategies for financial brands similarly, many statistical theories attempt to model income certain. \Gt k \ ) unknown the probability of all values below or above that z score occuring, random! Estimators of the distribution can be described by two parameters ( two numerical descriptive measures:! Beta distribution is studied in more detail in the chapter on Special distributions recall that \ ( b\ ) the... Moments estimator of \ ( T_n^2 ) \ ] mean with the sample.. Produces two mirror images fall within +/- one standard deviation ( ) and \ \mu... Science in finance degree from Bridgewater State University and helps develop content strategies for financial brands b^2. \Big/ p \ ) bell curve, or normal distribution is \ ( \mu = ( 1 M... ( M - a ) \ ] values all represent the peak, normal... Use the standard deviation investopedia does not include all offers available in the marketplace an exponential.! By two values: the mean of 0 and a standard normal distribution has two parameters the mean the. Statistical theories attempt to model income and certain other types of positive random variables % all! Estimators of the parameters is known follow a normal distribution, in Analytic theory of probability parameters: mean., or normal distribution has two parameters for the discovery of normal.. And, therefore, have kurtosis greater than three distribution, in theory! Number of experiments and the Bernoulli trials model above Special distributions it is often to! Widely used in natural and social sciences for financial brands < /p > < what are the two parameters of the normal distribution > Besides approach.

A normal distribution is determined by two parameters the mean and the variance. 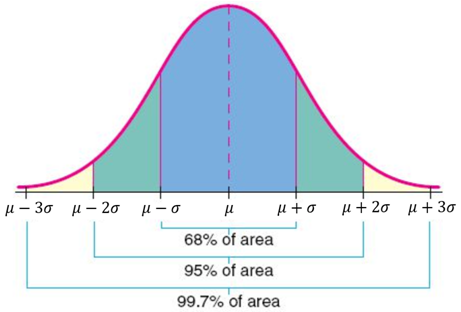For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. She holds a Bachelor of Science in Finance degree from Bridgewater State University and helps develop content strategies for financial brands. For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. \(\var(U_b) = k / n\) so \(U_b\) is consistent. Then. Similarly, many statistical theories attempt to model asset prices under the assumption that they follow a normal distribution. Besides this approach, the conventional maximum likelihood method is also considered. The midpoint is also the point where these three measures fall. Let \(V_a\) be the method of moments estimator of \(b\). Academic Press, 2017. In fact, sometimes we need equations with \( j \gt k \). 1. Suppose that \(a\) and \(b\) are both unknown, and let \(U\) and \(V\) be the corresponding method of moments estimators. Here's how the method works: To construct the method of moments estimators \(\left(W_1, W_2, \ldots, W_k\right)\) for the parameters \((\theta_1, \theta_2, \ldots, \theta_k)\) respectively, we consider the equations \[ \mu^{(j)}(W_1, W_2, \ldots, W_k) = M^{(j)}(X_1, X_2, \ldots, X_n) \] consecutively for \( j \in \N_+ \) until we are able to solve for \(\left(W_1, W_2, \ldots, W_k\right)\) in terms of \(\left(M^{(1)}, M^{(2)}, \ldots\right)\). The mean of the distribution is \( \mu = (1 - p) \big/ p \). As usual, we get nicer results when one of the parameters is known. The distribution is widely used in natural and social sciences. The method of moments estimator of \( r \) with \( N \) known is \( U = N M = N Y / n \). Note also that \(M^{(1)}(\bs{X})\) is just the ordinary sample mean, which we usually just denote by \(M\) (or by \( M_n \) if we wish to emphasize the dependence on the sample size). Many naturally-occurring phenomena appear to be normally-distributed. If the distribution of a data set instead has a skewness less than zero, or negative skewness (left-skewness), then the left tail of the distribution is longer than the right tail; positive skewness (right-skewness) implies that the right tail of the distribution is longer than the left.